What makes a number random?
Pick a random number between 1 and 10.
Was it 7?
Humans are really bad at picking random numbers. For instance, choosing 1 or 10 doesn’t seem so random because they are the largest and smallest numbers. A number picked near the middle intuitively feels more random than one at the higher or lower end. Even numbers seem less random than odd ones (though there is no reason for this to be true).
A true random number is equally likely to be any of the numbers and is completely independent of any previous number chosen. That means if you were to choose a large set of random numbers, each one would appear an equal number of times and it would be impossible to predict with absolute certainty the next few numbers. If you were to keep generating random numbers forever, you could produce any sequence of numbers (although this may take longer than the universe’s lifetime).
Why do we want random numbers?
For much of human history, random numbers were only used in games of chance. Dice go back 5,000 years (Piovano, 2011/2016). During WW2, random numbers became an important statistical tool for von Neuman when he was working on the Manhattan project (Metropolis, 1987) and for use by the Germans in sending encrypted messages.

From the Manhattan Project (Metropolis, 1987) came the Monte Carlo method. These are simulations that take a large number of samples from a model using random numbers to compute something that would be difficult to solve otherwise. They are a powerful and ubiquitous tool in physics, economics and data science. It became clear that random numbers were increasingly useful in areas of science, cryptography and statistics. More recently, with the abundance of private information sent over the internet, there is a considerable need to generate a large number of random numbers for various encryption standards (Zhou & Tang, 2011).
HOW DO CONVENTIONAL RNGs WORK
Computers generate random numbers in a deterministic way by taking a number that is close enough to being random (known as the seed) and then performing some iterative process to generate a sequence of numbers that appears random. For simple processes, the seed can be digits from the computers time in milliseconds.
Different algorithms generate the sequence in different ways. The middle square method used by von Neuman (Neuman, 1951) took a three-digit number, squared it, and took the middle three digits as the next number in the sequence. For instance, starting from 123, you compute 1232 = 15129 and just take 512 as the next number and repeat as long as needed.
Another method, the linear congruential method (Thomson, 1958), generates the next term by calculating:
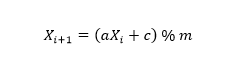
Where Xi+1 is the next term in the sequence, is the previous term, is the multiplier, is the increment and is the modulus. This sequence will repeat with a period less than m.
However, these methods are called Pseudorandom number generators (PRNGs) and do not actually produce random numbers. Anyone who knows the seed (initial random number) and the algorithm can generate the entire sequence with complete certainty. If left to run for long enough, both the middle square method and linear congruential method will repeat. This is fine for videogames where it is the feeling of randomness which matters, but not so great for encrypting communications (Li, 2013). With insider knowledge of the PRNG, an attacker could decrypt the communication.
QUANTUM RNG
Thankfully there are ways of generating truly random numbers based on physical processes. Atmospheric noise, the cosmic microwave background (the effect that caused static on old TVs) and radioactive decay are good examples. We can measure radio wave or microwave radiation, or the number of clicks from a Geiger counter.
Quantum computers can also be used for this purpose. They are effectively controlled physical experiments leveraging quantum mechanics to perform some computation. Since randomness is an inherent part of quantum mechanics, quantum computers, unlike classical ones used by von Neuman, can serve as a True Random Number Generator (TRNG) (Jacak, 2021). This is because a quantum system can exist in a superposition of possible states, and following a measurement takes on one of these states. Whilst we can know the probability of the system taking each of these states, we cannot know with absolute certainty which it will take (Nielsen & Chuang, 2000).
Below is an example of how n random numbers (from 0 to nmax) can be generated using IBM’s quantum computer. The code (can be found here) creates a quantum circuit with enough qubits to represent the power of 2 greater than nmax. The qubits are then put into a superposition and measured to obtain the random number. This process is repeated 1000 times and sampled n times to produce the numbers.
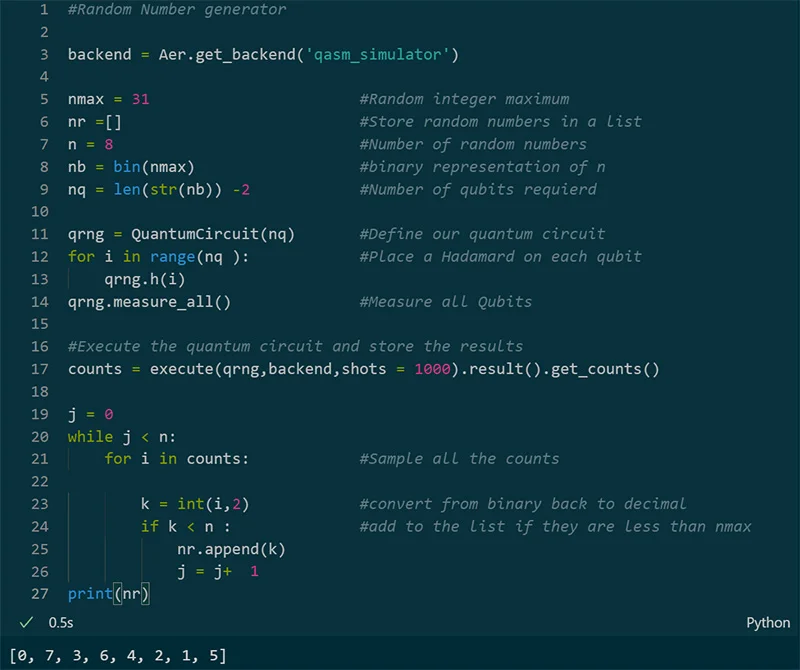
The TRNG implemented here is hardly the most practical implementation. It is rather slow, requires access to IBM’s cloud infrastructure, is vulnerable to interception, and runs on a device cooled to nearly absolute zero. A more useful implementation of this concept was done 20 years ago by the Swiss company ID Quantique, using a photonic chip. Newer models can be integrated in desktop PCs with PCIe connectivity or even USB (ID Quantique, n.d.).
REFERENCIAS
ID Quantique. (n.d.). Quantis QRNG Chip. Retrieved from https://www.idquantique.com/random-number-generation/products/quantis-qrng-chip/
Jacak, M. J. (2021). Quantum generators of random numbers. Sci Rep.
Li, A. (2013). Potential Weaknesses In Pseudorandom Number Generators.
Metropolis, N. (1987). The Beginning of the Monte Carlo Method. Los Alamos Science Special Issue, 15.
Neuman, J. v. (1951). Various Techniques Used in Connection With Random Digits. Res. Nat. Bur. Stand. Appl. Math.
Nielsen, M. A., & Chuang, I. L. (2000). Quantum Computation and Quantum Information. Cambridge University Press.
Piovano, I. (2011/2016). In Logic and Belief in Indian Philosophy. Warsaw Indological Studies.
Thomson, W. E. (1958). A Modified Congruence Method of Generating Pseudo-random Numbers. The Computer journal , 83.
Zhou, X., & Tang, X. (2011). Research and implementation of RSA algorithm for encryption and decryption. Research and implementation of RSA algorithm for encryption and decryption.

Thomas Clarke – Quantum Strategist

VISITA NUESTRO CENTRO DE CONOCIMIENTO
Creemos en el conocimiento democratizado
Conocimiento para todos: Infografías, blogs y artículos
Ataquemos las dificultades de tu negocio con tecnología
"Hay una gran diferencia entre lo imposible y lo difícil de imaginar. La primera tal vez lo es, la segunda se trata de ti"

Marvin Minsky, profesor pionero de la Inteligencia Artificial