
Have you ever been to the supermarket and wondered what was the most efficient path to find all your groceries? Or perhaps on holiday, have you ever wanted to plan a journey going through as many tourist attractions in the shortest route?

If you only have a few items on your list, this isn’t so hard. You might know the quickest way from the vegetables isle to the bakery, but what if your shopping list had a hundred items on it?
Then it becomes harder. The number of different ways you could plan your route gets really big as the number of items increases. For 5 items on a list, there are 120 different routes you could go. For 10 items, that becomes 362,880 different possible routes!
The Travelling Salesman
This type of problem is known as the traveling salesman problem (TSP), after its popular description in the 1930s [1] where a salesman has to find the shortest route to visit a list of cities. Variants of the TSP can be seen in many areas of business and science. A shipping company wanting to lower its operating costs might want to find the best route for shipping cargo to many different countries. In X-ray crystallography [2] a detector needs to measure the intensity of X-rays from many different positions on a sample. The order in which these measurements are made doesn’t matter, but repositioning the sample requires moving 4 motors, sometimes for hundreds of thousands of samples.
For a large number of destinations, or X-ray positions, it would be impractical to go through each possible pathway and find the shortest route (the brute-force approach). What this means is we can only try some of the paths and try to make our way to a good solution (not always the best one). There are a range of different algorithms you can use to do this, genetic algorithms, simulated annealing, tabu search, ant colony optimization, and cross-entropy method. Here we will only consider simulated annealing (SA).
How to solve the problem
Simulated annealing is an optimization method inspired by metallurgy, a process that heats and cools a metal to improve its physical properties. To get a solution to our TSP, we start from some random path (we shuffle all the cities on our list), and then make changes to our path for some period of time. First, we calculate the total distance across our path by adding up all the distances from each pair of cities. Then, we propose a new path, which is the same as the old path, but we swap at random two of the cities along with the list.
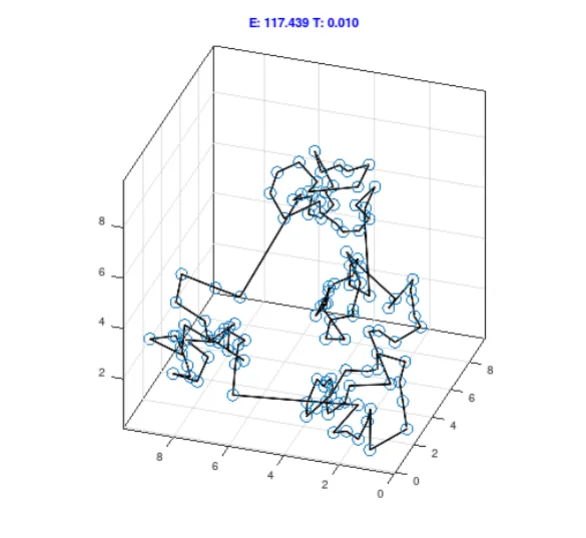
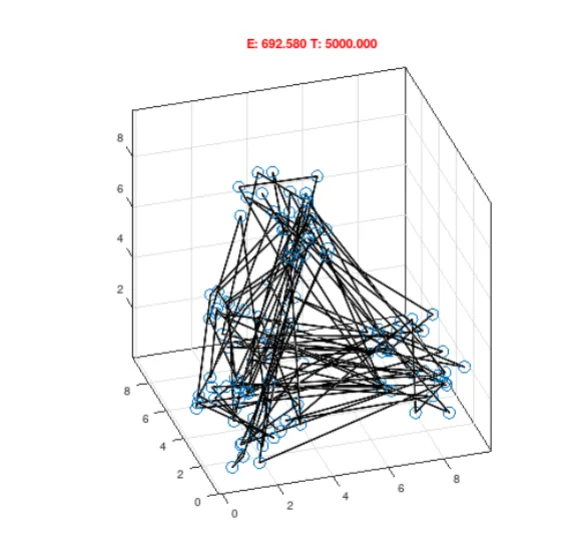
Depending on whether the new path is longer than the old path, we accept or reject it with a probability. If we accept the new path, the old path is replaced by the new path. We repeat this proposal process for many iterations and eventually, we reach a path that is much better than the random one we started with. The diagrams below [3] show an example of annealing for points in a 3D grid. The process starts from the image on the left, and after the annealing process, the right.
Why quantum?
So, where does quantum come in? Quantum annealing (QA) follows a similar approach to SA, but it optimizes a quantum system instead of a classical system in the case of SA [5]. To do QA, you need a quantum computer known as a quantum annealer. The main difference between QA and SA is that QA maps our problem (finding the best route) to finding the lowest energy state of a physical system. This allows us to use some phenomena from quantum mechanics to potentially solve our problem faster.
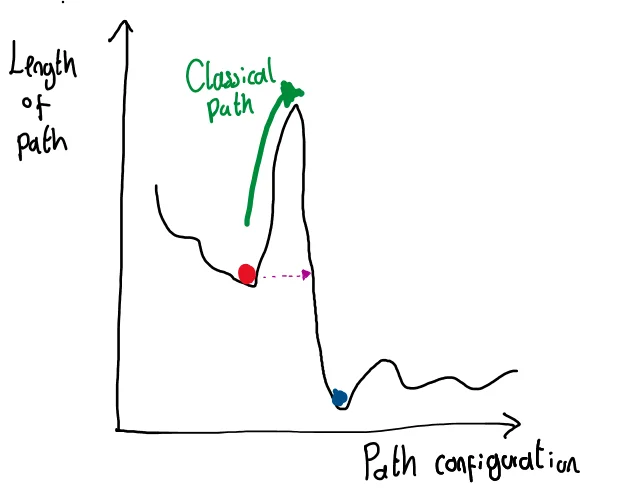
With SA, the space of possible solutions is sampled one at a time. With QA, we can start from a great many possible paths at once. This is known as a superposition and effectively allows us to consider a greater number of paths at one time. QA also takes advantage of quantum tunneling, a phenomenon in which a quantum system has a probability of escaping local minima. In the diagram, we see how this works. Starting from the red path we want to get to the blue path but the paths in between have a significant increase in length. Using SA it is very unlikely for the classical path (green) because the increase in length is so great. But with QA, we have a probability of tunneling through (purple) to get to the blue path.
Whilst theoretically this is great, there are a few limitations in practice. Firstly, the quantum annealers of today are relatively small scale. As of the time of writing, only a path of 9 cities has been solved [9] which is orders of magnitude less than the world record for over a million cities that can be done on powerful supercomputers [6]. That said, the company that makes quantum annealers, D-Wave, lists over 250 early applications of QA including traffic flow optimization and waste collection optimization for sustainable cities [7].
For more information on the traveling salesman problem, click here. If you’d like to learn more about quantum annealing, I recommend you check out the description from D-Wave.
If you want to know more about Quantum Computing read my blog Random Number Generators.
REFERENCES
[1] Grötschel, M., Holland, O. Solution of large-scale symmetric traveling salesman problems. Mathematical Programming 51, 141–202 (1991). https://doi.org/10.1007/BF01586932
[2] Lawler, E. L. (1985). The Travelling Salesman Problem: A Guided Tour of Combinatorial Optimization (Repr. with corrections. ed.). John Wiley & sons. ISBN 978-0471904137.
[3] Original image by Panchotera~enwiki – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=101533459
[4] Arnab Das (Theoretical Condensed Matter Physics Division and Centre for Applied Mathematics and Computational Science, Saha Institute of Nuclear Physics, Kolkata, India) – Quantum Annealing and Other Optimization Methods workshop, 2005
[5] Warren, R.H. Solving the traveling salesman problem on a quantum annealer. SN Appl. Sci. 2, 75 (2020). https://doi.org/10.1007/s42452-019-1829-x
[6] http://www.math.uwaterloo.ca/tsp/world/
[7] Sheir Yarkoni, Florian Neukart, Eliane Moreno Gomez Tagle, Nicole Magiera, Bharat Mehta, Kunal Hire, Swapnil Narkhede, and Martin Hofmann. 2020. Quantum Shuttle: traffic navigation with Quantum computing. In Proceedings of the 1st ACM SIGSOFT International Workshop on Architectures and Paradigms for Engineering Quantum Software (APEQS 2020). Association for Computing Machinery, New York, NY, USA, 22–30. DOI:https://doi.org/10.1145/3412451.3428500

Thomas Clarke – Quantum Strategist

VISIT OUR KNOWLEDGE CENTER
We believe in democratized knowledge
Understanding for everyone: Infographics, blogs, and articles
Let’s tackle your business difficulties with technology
” There’s a big difference between impossible and hard to imagine. The first is about it; the second is about you “

Marvin Minsky, Professor pioneer in Artificial Intelligence